Den romerske arkitekt og ingeniør Marcus Vitruvius Pollio, der levede i første århundrede f. Kr., regnes for at være den, der har formuleret 'Loven om det gyldne snit'. Det er en kompositionsform, som utallige billedkunstnere har fulgt eller i hvert fald ladet sig inspirere af, når de skulle bygge deres billedværk op. Marcus Vitruvius Pollio citeres for bl.a. at have sagt:
For at få en æstetisk tiltalende ulige inddeling af et givent rum, må den mindste del forholde sig til den større, som den større del forholder sig til helheden.
Kilde: Matematik i kunsten af Eigil Peter Hansen, Munksgaard 1993, s. 38.
Den såkaldte gyldne brøk er en matematisk formel, der lyder således:
- enten kvadratroden af 5 minus 1 divideret med 2 = 0, 6180339
- eller kvadratroden af 5 plus 1 divideret med 2 = 1, 6180339
Hvis man dividerer to tal, der står ved siden af hinanden i den såkaldte Fibonaccis talrække, så får man netop tilnærmelsesvist ovennævnte facitter. Fibonaccis talrække består af tal, der er kendetegnet ved, at fra og med det tredje tal fremkommer tallene som summen af de to foregående - og således fortsætter talrækken i det uendelige:
1 - 1 - 2 - 3 - 5 - 8 - 13 - 21 - 34 - 55 - 89 - 144 - 233 - 377 - 610 - osv.
Når vi taler om den gyldne brøk i forbindelse med billedkomposition, skal det altså forstås på den måde, at hvis former eller linjer er proportioneret (delt) sådan, at den største størrelse divideret med den mindste tilnærmelsesvist giver et tal i nærheden af 1,6180339 (fx 5:3=1,666667, 13:8=1,625, 233:144=1,6180555 osv.), så er formen eller linjen komponeret efter den gyldne brøk.
Denne linje er således delt ud fra den gyldne brøks princip:
En sådan kompositionsform (som i øvrigt er ganske almindelig i mange af naturens organismer, fx mange blomster) skulle altså give beskueren en forstærket oplevelse af harmoni og æstetisk (skønhedsmæssig) nydelse.
Hvis vi undersøger om den gyldne brøk er bragt i anvendelse i et billedes komposition, er det især følgende forhold, vi skal være opmærksomme på:
- Det gyldne rektangel
- Det gyldne snit
- Et gyldent rektangel er der tale om, hvis selve billedets ydre ramme eller hvis mere eller mindre synlige rektangelformer i billedet har proportioner, hvor den korte side i rektanglet divideret med den længste tilnærmelsesvis er ca. 0,618... eller den længste side divideret med den korteste er tæt på 1,618...
- Det gyldne snit taler man om, når særlige eller vigtige billedelementer er placeret i nogle bestemte 'snit' i en billedflade. Og placeringen af disse snit har også med den gyldne brøk at gøre.
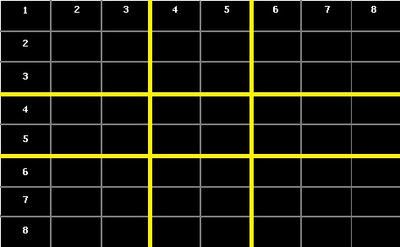
Hvis du vil undersøge om særlige billedelementer er placeret i et eller flere af billedfladens gyldne snit, kan du måle ca. tre ottendedele af hver sides længde ind fra alle rektanglets fire sider og tegne vinkelrette linjer der:
De punkter, de gyldne snitlinjer skærer hinanden i, kaldes 'gyldne punkter':
Se illustrationerne herunder: